Job shop scheduling in python
Job shop scheduling is problem where the user has to schedule multiple jobs on multiple machines. At a small scale it is easy enough to solve by hand. But when the number of jobs and available machines is relatively large, it is almost impossible to solve by hand. In computer science it is known as an NP-Complete Problem. In technical terms for every instance of the job shop scheduling problem with more than 3 available machines there no known exact algorithms that can solve it in polynomial time.
NP-Completness is a great excuse for any scientist, when faced with a problem too difficult to solve, to prove it is NP-Complete and get of scot free when the algorithm takes a long time to solve the problem. In layman terms there is no guarantee that for many jobs on many machines you will be able to find an optimal schedule quickly.

In reality, hardware and software has come a long way since when the JSSP was formulated as mathematical optimization problem. Bob Bixby has a nice slide in one of his talks where he showcases the improvement in solver technology. This means that relatively large scheduling instances can be solved to optimality or close to optimality in short time.
One interesting technology to solve scheduling problems is Constraint Programming. The origins of CP are in the field of artifical intelligence. CP provides language and techniques which allow a user to create models for comlex tasks.
In this blog I will be using the CP-SAT from Google OR-Tools. Google’s OR-Tools is an open source tool which can be used to solved many optimizatiom problems. They won gold medals at the MiniZinc 2020 competition(It’s a well-respected competition amongst people interested in solving constraint programming problems).
Import the relevant libraries
We use pandas for storing the output and plotly for plotting the Gantt chart.
import collections
from ortools.sat.python import cp_model
import plotly.figure_factory as ff
import pandas as pd
Define the jobs data
Every job is a series of tasks that must be performed sequentially.
Every task is a pair of machine on which it can be processed and the processing time.
Task 1 = (0,125)
Here task 1 is set to be processed on machine_id 0 and takes 125 minutes.
I am creating a fictional factory that manufactures “widgets”. There are 4 stages to manufacturing widgets. The orders and processing steps are as below:
| Process step | Order 1 (Widget A) | Order 2 (Widget B) | Order 3 (Widget C) | Order 4 (Widget D) |
|---|---|---|---|---|
| Step 1 | (0,500) | (0,2000) | (0,1000) | (0,750) |
| Step 2 | (1,250) | (1,2500) | (1,750) | (1,100) |
| Step 3 | (2,500) | (2,3000) | (2,1000) | (2,750) |
| Step 4 | (3,100) | (3,1000) | (3,750) | (3,500) |
We have 4 orders to fulfill and we have 4 machines to process the orders.
#Read in the order data from a CSV file
jobs_df = pd.read_csv(r'D:\Data Science\Discrete Optimization\Order_data_blog.csv')
#jobs_df.head()
#Create a tuples of machine_id and processing time
job1 = list(jobs_df[['Machine_ID', 'Processing Time (in minutes)']].itertuples(index=False, name=None))
job2 = list(jobs_df[['Machine_ID.1', 'Processing Time (in minutes).1']].itertuples(index=False, name=None))
job3 = list(jobs_df[['Machine_ID.2', 'Processing Time (in minutes).2']].itertuples(index=False, name=None))
job4 = list(jobs_df[['Machine_ID.3', 'Processing Time (in minutes).3']].itertuples(index=False, name=None))
#Create nested list for all the sales orders
jobs_data = [job1,job2,job3,job4]
#Get the number of machines in the jobs_data list using list comprehension
machines_count = 1 + max(task[0] for job in jobs_data for task in job)
all_machines = range(machines_count)
#Calculate the horizon as the summ of all durations
#This sets a limit on maximum time our schedule can take
horizon = sum(task[1] for job in jobs_data for task in job)
Define the variables
When solving the JSSP there some common constraints across all instances.
-
Precedence constraint
Precedence constraint is where a task can only start after the preceding task has been completed. You can only wear shoes after you have put on your socks! A variation of the precedence constraint is that there should be atleast some time difference between two tasks. If you are scheduling jobs in a paint shop then you want to add drying time between tasks. -
Overlap constraint
No overlap constraint ensures that a machine works on only one task at a time. Two tasks should not be scheduled on a machine at the same time.
Syntax for the variables
I used two variables in the code below : NewIntVar and NewIntervalVar
Syntax for NewIntVar is (self, lower bound, upper bound, name)
NewIntVar is used to denote the start and end of any particular task. The upper bound is set as the horizon to constrain the problem size to a finite domain.
Sidenote : CP-SAT solver can only process integer variables. No fractional variables are allowed.
Constraints are added to the model using the Add method. It adds a bounded linear expression to the model.
The second variable is the NewIntervalVar
Syntax for NewIntervalVar is (self, start, size, end, name)
From the documentation:
An interval variable is a constraint, that is itself used in other constraints like NoOverlap.
Internally, it ensures that start + size == end.
# Named tuple to store information about created variables.
task_type = collections.namedtuple('task_type', 'start end interval')
# Named tuple to manipulate solution information.
assigned_task_type = collections.namedtuple('assigned_task_type',
'start job index duration')
# Creates job intervals and add to the corresponding machine lists.
all_tasks = {}
machine_to_intervals = collections.defaultdict(list)
for job_id, job in enumerate(jobs_data):
for task_id, task in enumerate(job):
machine = task[0]
duration = task[1]
suffix = '_%i_%i' % (job_id, task_id)
start_var = model.NewIntVar(0, horizon, 'start' + suffix)
end_var = model.NewIntVar(0, horizon, 'end' + suffix)
interval_var = model.NewIntervalVar(start_var, duration, end_var,
'interval' + suffix)
all_tasks[job_id, task_id] = task_type(start=start_var,
end=end_var,
interval=interval_var)
machine_to_intervals[machine].append(interval_var)
Define the constraints
First the disjunctive constraints to ensure the no machine is assigned two jobs at the same time. The syntax for AddNoOverlap is (self, interval_vars).
interval_vars: The list of interval variables to constrain.
Now, the precedence constraints inside the jobs. We also want that between two manufacturing stages there should be a atleast 90 minutes.
# Create and add disjunctive constraints.
for machine in all_machines:
model.AddNoOverlap(machine_to_intervals[machine])
# Precedences inside a job.
for job_id, job in enumerate(jobs_data):
for task_id in range(len(job) - 1):
model.Add(all_tasks[job_id, task_id +
1].start >= all_tasks[job_id, task_id].end + 90)
Define the objective
Usually the objective is to minimize the ‘makespan’. Makespan is the total length of the schedule.
We create a variable obj_var whose value is the maximum of the end times for all jobs i.e the makespan.
In practical settings, the objective can be somewhat different. We might be interested in ensuring that all the jobs are served on time or that the utilization for some machine is below 80%.
# Makespan objective.
obj_var = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(obj_var, [
all_tasks[job_id, len(job) - 1].end
for job_id, job in enumerate(jobs_data)
])
model.Minimize(obj_var)
Solve the model
# Creates the solver and solve.
solver = cp_model.CpSolver()
status = solver.Solve(model)
Post processing and visualization
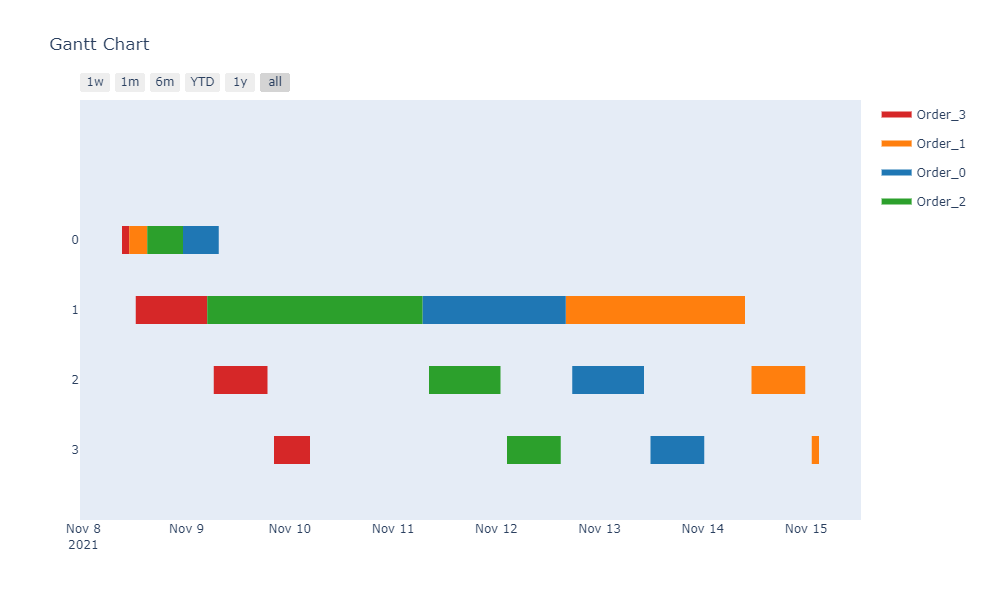
Visualization is a very important step to to understand the output of the model. The standard template to visualize schedules is a Gantt chart. I have used plotly to create the Gantt chart.
plan_date = pd.to_datetime('11/08/2021 09:00:00')
def visualize_schedule(assigned_jobs,all_machines,plan_date):
final = []
for machine in all_machines:
assigned_jobs[machine].sort()
for assigned_task in assigned_jobs[staff]:
name = 'Order_%i' % assigned_task.job
temp = dict(Task=staff,Start=plan_date + pd.DateOffset(minutes = assigned_task.start),
Finish= plan_date + pd.DateOffset(minutes = (assigned_task.start + assigned_task.duration)),
Resource=name)
final.append(temp)
final.sort(key = lambda x: x['Task'])
return final
Complete script
"""Minimal jobshop example."""
import collections
from ortools.sat.python import cp_model
plan_date = pd.to_datetime('11/08/2021 09:00:00')
def visualize_schedule(assigned_jobs,all_staffs,plan_date):
final = []
for machine in all_machines:
assigned_jobs[machine].sort()
for assigned_task in assigned_jobs[machine]:
name = 'Order_%i' % assigned_task.job
temp = dict(Task=staff,Start=plan_date + pd.DateOffset(minutes = assigned_task.start),
Finish= plan_date + pd.DateOffset(minutes = (assigned_task.start + assigned_task.duration)),
Resource=name)
final.append(temp)
final.sort(key = lambda x: x['Task'])
return final
def main():
"""Minimal jobshop problem."""
# Data.
#Read in the order data from a CSV file
jobs_df = pd.read_csv(r'D:\Data Science\Discrete Optimization\Order_data_blog.csv')
#jobs_df.head()
#Create a tuples of machine_id and processing time
job1 = list(jobs_df[['Machine_ID', 'Processing Time (in minutes)']].itertuples(index=False, name=None))
job2 = list(jobs_df[['Machine_ID.1', 'Processing Time (in minutes).1']].itertuples(index=False, name=None))
job3 = list(jobs_df[['Machine_ID.2', 'Processing Time (in minutes).2']].itertuples(index=False, name=None))
job4 = list(jobs_df[['Machine_ID.3', 'Processing Time (in minutes).3']].itertuples(index=False, name=None))
#Create nested list for all the sales orders
jobs_data = [job1,job2,job3,job4]
machines_count = 1 + max(task[0] for job in jobs_data for task in job)
all_machines = range(machines_count)
# Computes horizon dynamically as the sum of all durations.
horizon = sum(task[1] for job in jobs_data for task in job)
print(horizon)
# Create the model.
model = cp_model.CpModel()
# Named tuple to store information about created variables.
task_type = collections.namedtuple('task_type', 'start end interval')
# Named tuple to manipulate solution information.
assigned_task_type = collections.namedtuple('assigned_task_type',
'start job index duration')
# Creates job intervals and add to the corresponding machine lists.
all_tasks = {}
machine_to_intervals = collections.defaultdict(list)
for job_id, job in enumerate(jobs_data):
for task_id, task in enumerate(job):
machine = task[0]
duration = task[1]
suffix = '_%i_%i' % (job_id, task_id)
start_var = model.NewIntVar(0, horizon, 'start' + suffix)
end_var = model.NewIntVar(0, horizon, 'end' + suffix)
interval_var = model.NewIntervalVar(start_var, duration, end_var,
'interval' + suffix)
all_tasks[job_id, task_id] = task_type(start=start_var,
end=end_var,
interval=interval_var)
machine_to_intervals[machine].append(interval_var)
# Create and add disjunctive constraints.
for machine in all_machines:
model.AddNoOverlap(machine_to_intervals[machine])
# Precedences inside a job.
for job_id, job in enumerate(jobs_data):
for task_id in range(len(job) - 1):
model.Add(all_tasks[job_id, task_id +
1].start >= all_tasks[job_id, task_id].end + 90)
# Makespan objective.
obj_var = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(obj_var, [
all_tasks[job_id, len(job) - 1].end
for job_id, job in enumerate(jobs_data)
])
model.Minimize(obj_var)
# Creates the solver and solve.
solver = cp_model.CpSolver()
status = solver.Solve(model)
if status == cp_model.OPTIMAL:
print('Solution:')
# Create one list of assigned tasks per machine.
assigned_jobs = collections.defaultdict(list)
for job_id, job in enumerate(jobs_data):
for task_id, task in enumerate(job):
machine = task[0]
assigned_jobs[machine].append(
assigned_task_type(start=solver.Value(
all_tasks[job_id, task_id].start),
job=job_id,
index=task_id,
duration=task[1]))
# Finally print the solution found.
print(f'Optimal Schedule Length: {solver.ObjectiveValue()}')
#print(output)
else:
print('No solution found.')
res = visualize_schedule(assigned_jobs,all_machines,plan_date)
fig = ff.create_gantt(res, index_col='Resource', show_colorbar=True, group_tasks=True)
fig.show()
# Finally, print the solution found.
print('Optimal Schedule Length: %i' % solver.ObjectiveValue())
if __name__ == '__main__':
main()